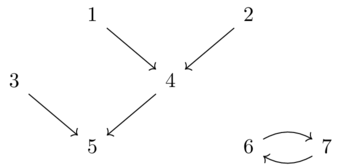
We want to convert this state information into a graph that will let us visualize our machine.
Use the following functor \(F\):
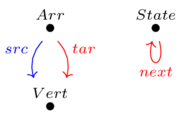
src is sent to identity
Can now generate a graph using the composite functor \(\mathbf{Gr}\xrightarrow{F}\mathbf{DDS}\xrightarrow{I}\mathbf{Set}\)